一、冒泡排序

  冒泡排序（Bubble Sort）是一种基础的排序算法，其核心思想是通过重复遍历列表，比较相邻元素，并根据需要交换位置，从而逐步将未排序部分的最大值“冒泡”到正确位置。下面是关于冒泡排序的详细介绍，包括原理、Python实现及复杂度分析。

1.1 冒泡排序基本原理

  冒泡排序的基本步骤如下：

1. 从头到尾遍历列表，比较相邻元素；
2. 如果前一个元素 > 后一个元素，则交换这两个元素；
3. 每完成一轮遍历，这一轮最大的元素会被冒泡至列表末尾；
4. 重复上述步骤，每次遍历减少一个待排序元素（已排序元素不再处理），对于 n 个元素的列表来说需要 n-1 次冒泡

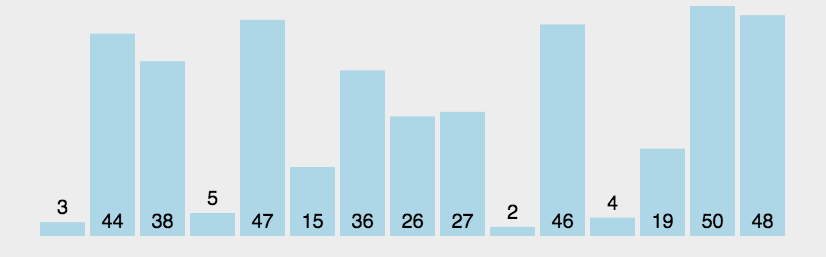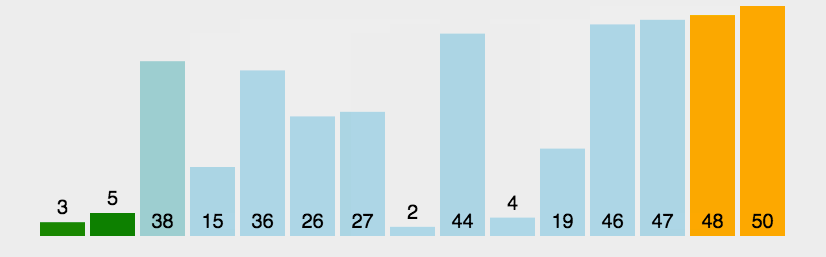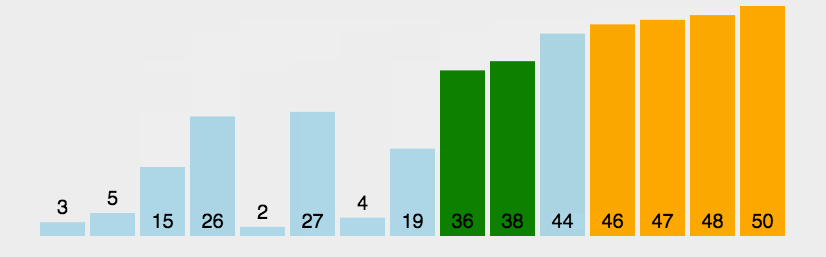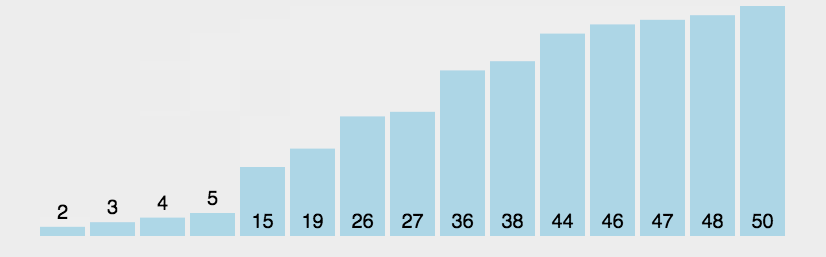
1.2 冒泡排序代码实现

冒泡排序的Python代码实现bubble_sort函数如下：

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr
​
​
lst = [10, 9, 6, 3, 5, 2, 4, 1, 7, 8]
print(bubble_sort(lst))

1.3 冒泡排序复杂度分析

时间复杂度分析

情况	时间复杂度	说明
最坏情况	O(n^2)	列表完全逆序，需全比较+交换
平均情况	O(n^2)	一般随机数据
最好情况	O(n)	列表已有序，一轮遍历即可退出

空间复杂度分析

  因其原地排序，仅占用常数级的额外空间，因此冒泡排序的空间复杂度为 O(1)。

二、插入排序

  插入排序（Insertion Sort）是一种简单直观的排序算法，它的核心思想是将数组分为已排序部分和未排序部分，然后逐步从未排序部分取出元素，插入到已排序部分的合适位置。

2.1 插入排序基本原理

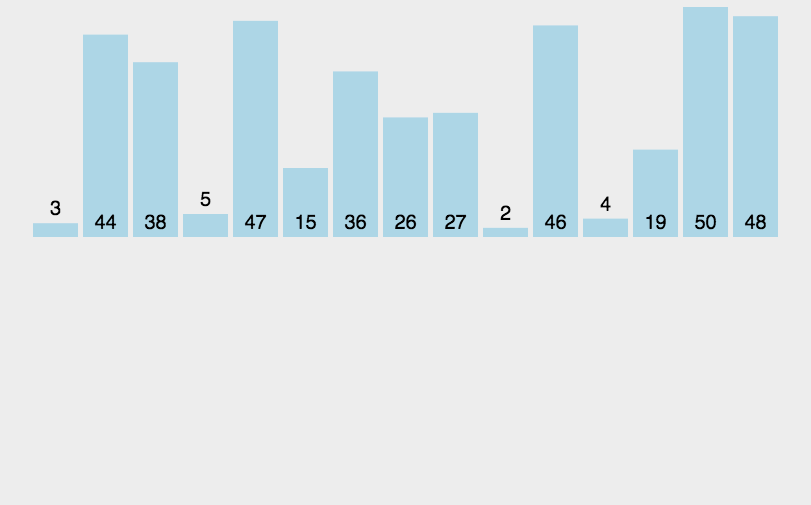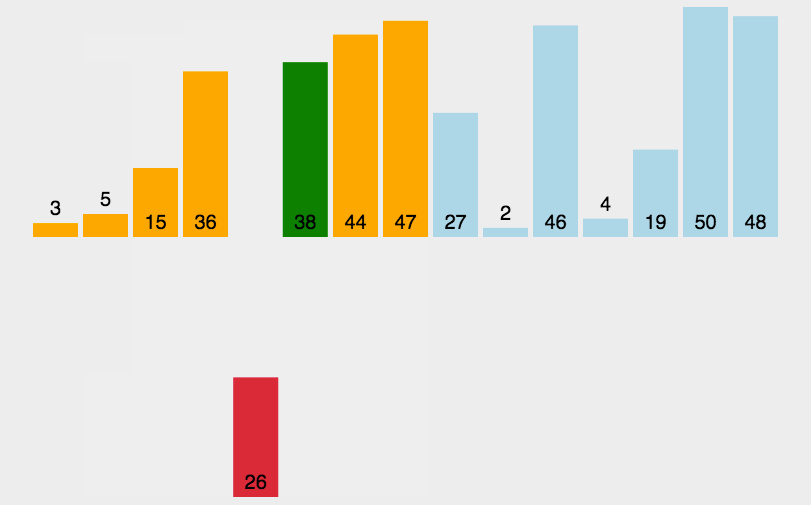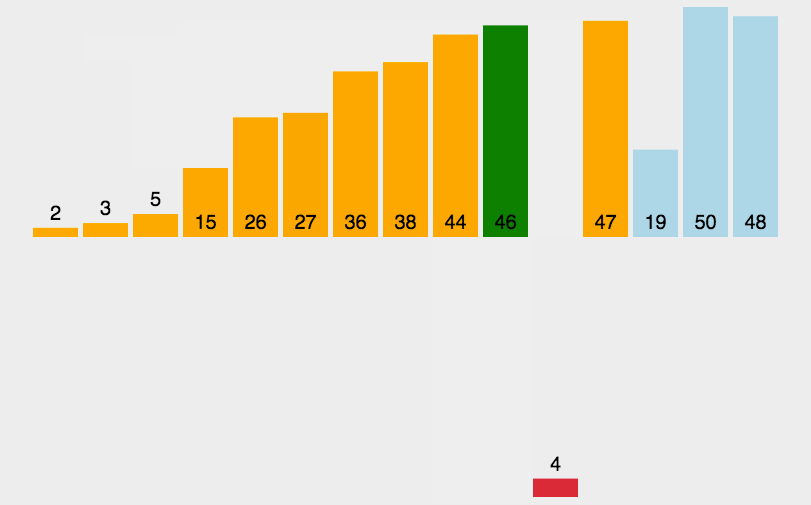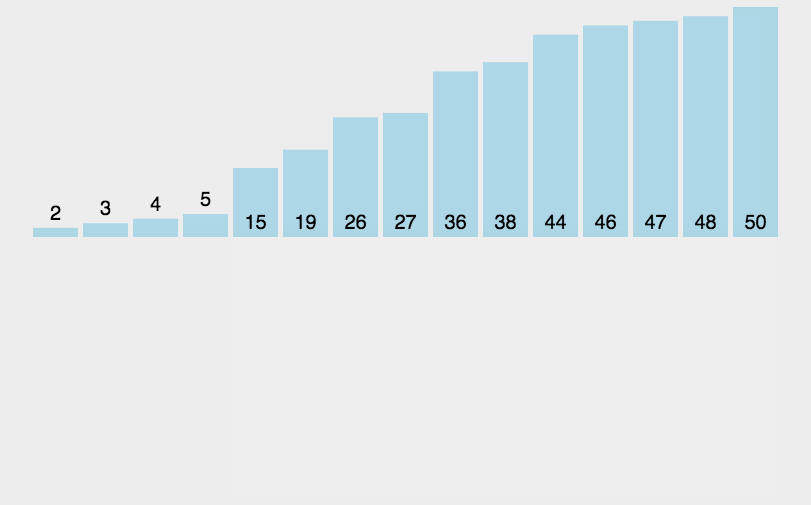
  插入排序的步骤如下：

1. 从第二个元素（索引 1）开始，将其视为当前要插入的元素 key；
2. 依次与前面已排序部分的元素进行比较，如果前面的元素比 key 大，则将其后移；
3. 找到 key 应该插入的位置，将其放入正确的位置；
4. 重复上述过程，直到所有元素都插入到正确的位置，数组排序完成

2.2 插入排序代码实现

插入排序的Python代码实现insert_sort函数如下：

def insert_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr
​
​
lst = [10, 9, 6, 3, 5, 2, 4, 1, 7, 8]
print(insert_sort(lst))

2.3 插入排序复杂度分析

时间复杂度分析

情况	时间复杂度	说明
最坏情况	O(n^2)	数组是完全逆序时，每个元素都要向前移动 i 次
平均情况	O(n^2)	数据是随机分布时，元素大约移动一半的位置
最好情况	O(n)	数组已经是有序时，每个元素只需进行一次比较

空间复杂度分析

  插入排序是原地排序算法（In-place Sorting），它只使用了常数级别的额外空间，即 O(1) 的空间复杂度。

三、选择排序

  选择排序（Selection Sort）是一种简单直观的排序算法，它的核心思想是 每次从未排序部分中选择最小（或最大）的元素，并将其放在已排序部分的末尾。

3.1 选择排序基本原理

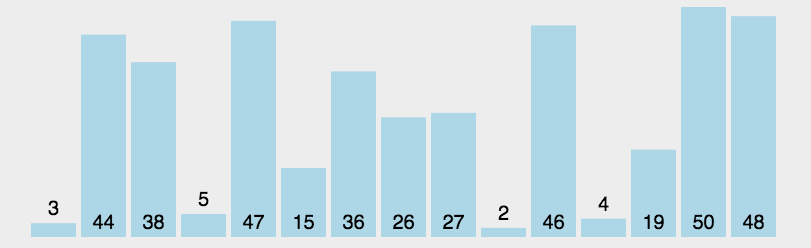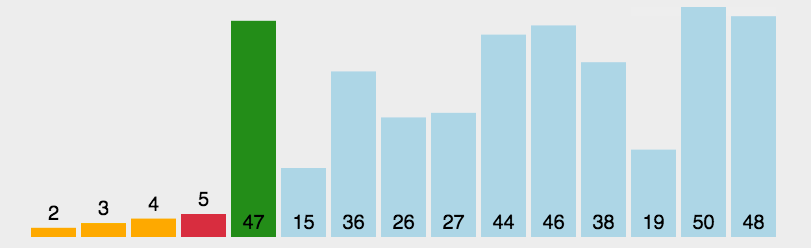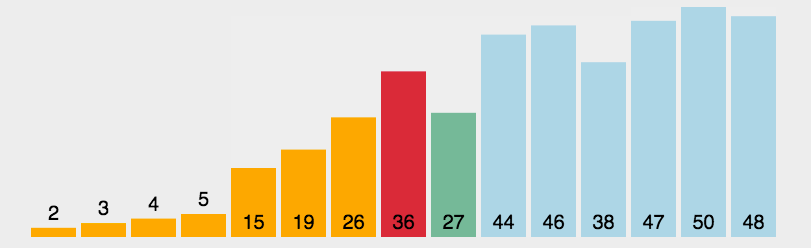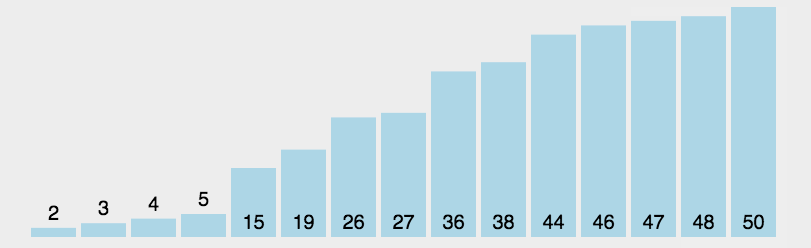
  选择排序的基本步骤如下：

1. 在数组中找到最小的元素，将其与数组的第一个元素交换；
2. 在剩下未排序的数组中找到最小的元素，将其与第二个元素交换；
3. 重复该过程，直到所有元素都排序完成

3.2 选择排序代码实现

选择排序的Python代码实现selection_sort函数如下：

def selection_sort(arr):
    n = len(arr)
    for i in range(n - 1):
        min_index = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_index]:
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]
    return arr
​
​
lst = [10, 9, 6, 3, 5, 2, 4, 1, 7, 8]
print(selection_sort(lst))

3.3 选择排序复杂度分析

时间复杂度分析

情况	时间复杂度	说明
最坏情况	O(n^2)	扫描整个未排序部分，并找到最小元素
平均情况	O(n^2)	始终进行 n(n-1)/2 次比较
最好情况	O(n^2)	数组已经有序，每轮仍然需要比较 n-i-1 次

空间复杂度分析

  同冒泡排序和插入排序一样，选择排序只使用了常数级别的额外空间，即 O(1) 的空间复杂度。

四、快速排序

  快速排序（Quick Sort）是一种基于分治（Divide and Conquer）思想的排序算法。

4.1 快速排序基本原理

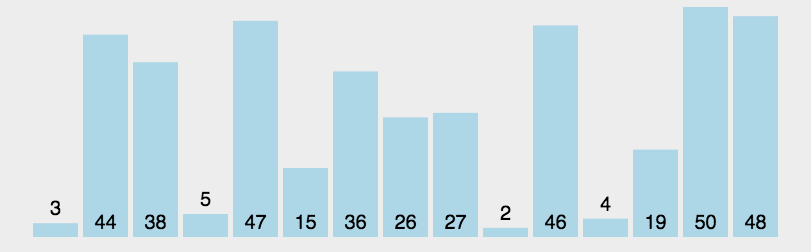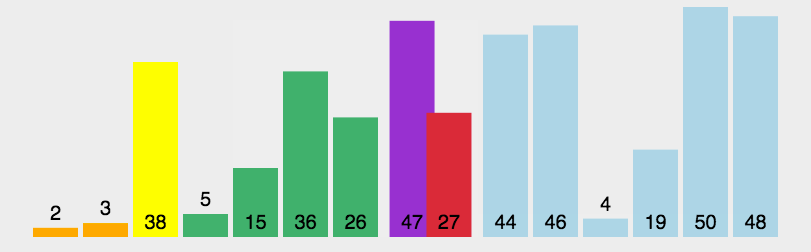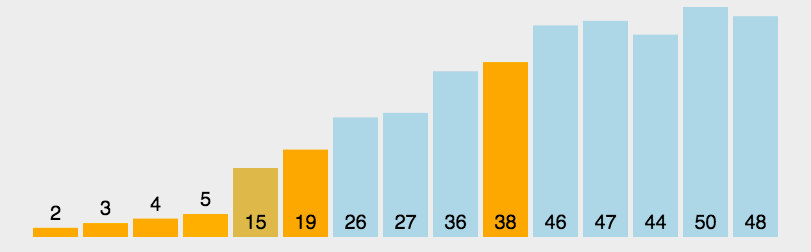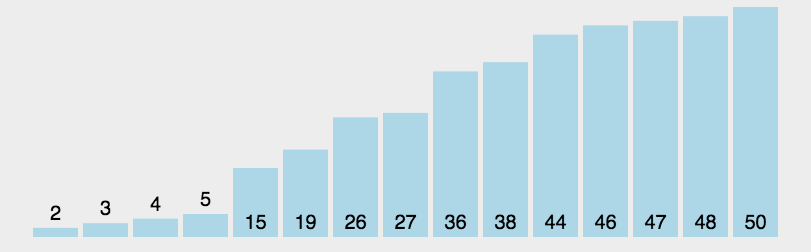
  快速排序的基本步骤如下：

1. 选择一个基准值pivot，通常是数组中的一个元素；
2. 将数组分成两个子数组，左侧的元素比基准值pivot小，右侧的元素要比基准值pivot大；
3. 递归地对左右两个子数组分别进行快速排序，直到子数组长度为1或0（无需再排序）

4.2 快速排序代码实现

快速排序的Python代码实现quick_sort函数如下：

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)
​
​
lst = [10, 9, 6, 3, 5, 2, 4, 1, 7, 8]
print(quick_sort(lst))

4.3 快速排序复杂度分析

时间复杂度

情况	时间复杂度	说明
最坏	O(n^2)	若每次 pivot 选择不当（如总是选取最大/最小值），导致分区极端不平衡
平均情况	O(nlogn)	在多数情况下，pivot 的选择不会极端不均匀
最好	O(nlogn)	若 pivot 选择合理，使得每次都均匀分区，递归深度为 log n，每层的操作是 O(n)。

空间复杂度

• 普通递归实现：需要 O(log n) 额外栈空间（递归调用栈深度）。
• 原地分区版本：空间复杂度可以优化到 O(1)。

Lomuto分区以及快速排序代码

def partition(arr, low, high):
    pivot = arr[high]
    i = low - 1
​
    for j in range(low, high):
        if arr[j] <= pivot:
            i += 1
            arr[i], arr[j] = arr[j], arr[i]
    arr[i + 1], arr[high] = arr[high], arr[i + 1]
    return i + 1
​
​
def quick_sort_inplace(arr, low, high):
    if low < high:
        pi = partition(arr, low, high)
        quick_sort_inplace(arr, low, pi - 1)
        quick_sort_inplace(arr, pi + 1, high)
​
lst = [10, 9, 6, 3, 5, 2, 4, 1, 7, 8]
quick_sort_inplace(lst, 0, 9)
print(lst)

五、归并排序

  归并排序（Merge Sort）是一种基于分治（Divide and Conquer）思想的排序算法。它采用递归的方法，将数组不断拆分成更小的部分，最终合并成一个有序的数组。

5.1 归并排序基本原理

  归并排序的基本步骤如下：

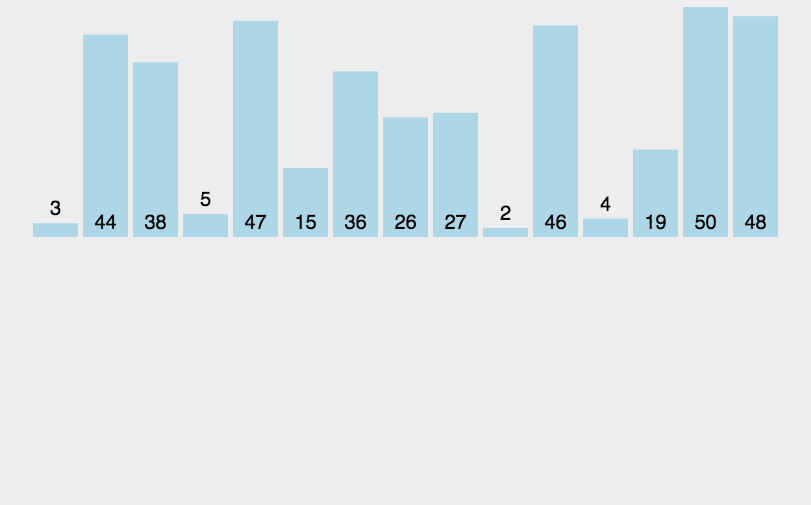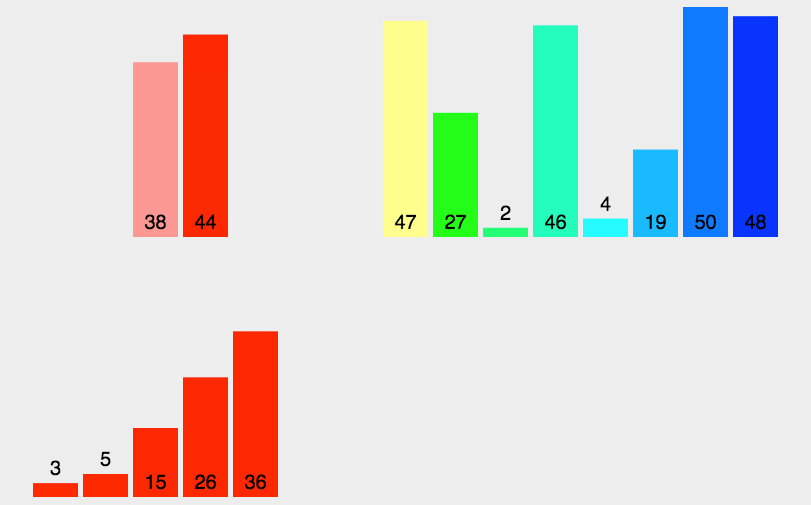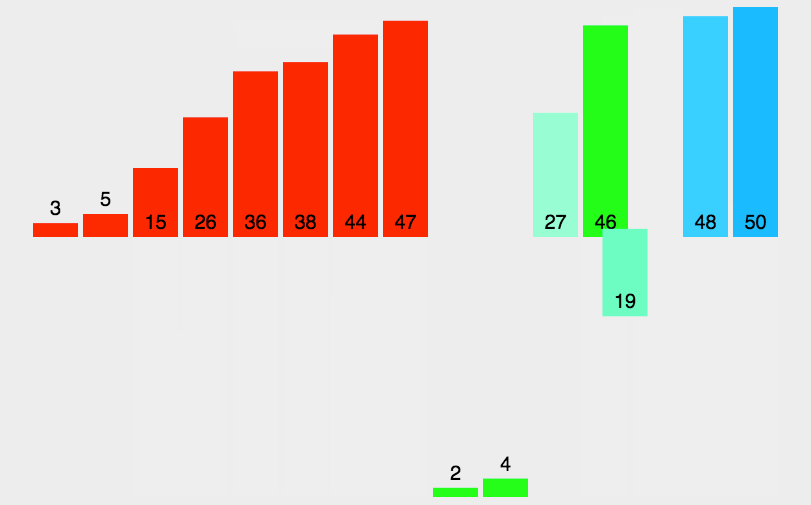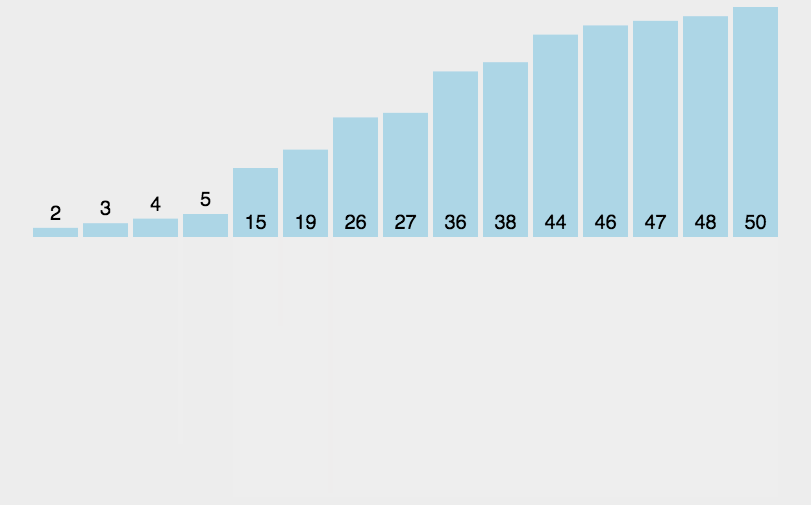
1. 分解：递归地将数组分成两个子数组，直到每个数组的长度为1；
2. 合并：逐步将两个子数组合并为一个有序数组，直到最终所有子数组都合并为一个完整的有序数组

5.2 归并排序代码实现

归并排序Python实现merge_sort函数如下：

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)
​
​
def merge(left, right):
    result = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])
    result.extend(right[j:])
    return result
​
​
lst = [10, 9, 6, 3, 5, 2, 4, 1, 7, 8]
print(merge_sort(lst))

5.3 归并排序复杂度分析

时间复杂度

情况	时间复杂度	说明
最坏情况	O(nlogn)	最好、平均、最坏情况一致
平均情况	O(nlogn)	\
最好情况	O(nlogn)	\

空间复杂度

  归并排序不是原地排序算法，它需要额外的 O(n) 空间来存储合并过程中的子数组。递归调用栈的深度最多为 log n，但主要的空间消耗来自于额外的临时数组。即其空间复杂度为 O(n)。